
“What is a p-value?” are words often uttered by early career researchers and sometimes even by more experienced ones. The p-value is an important and frequently used concept in quantitative research. It can also be confusing and easily misused. In this article, we delve into what is a p-value, how to calculate it, and its statistical significance.
What is a p-value
The p-value, or probability value, is the probability that your results occurred randomly given that the null hypothesis is true. P-values are used in hypothesis testing to find evidence that differences in values or groups exist. P-values are determined through the calculation of the test statistic for the test you are using and are based on the assumed or known probability distribution.
For example, you are researching a new pain medicine that is designed to last longer than the current commonly prescribed drug. Please note that this is an extremely simplified example, intended only to demonstrate the concepts. From previous research, you know that the underlying probability distribution for both medicines is the normal distribution, which is shown in the figure below.
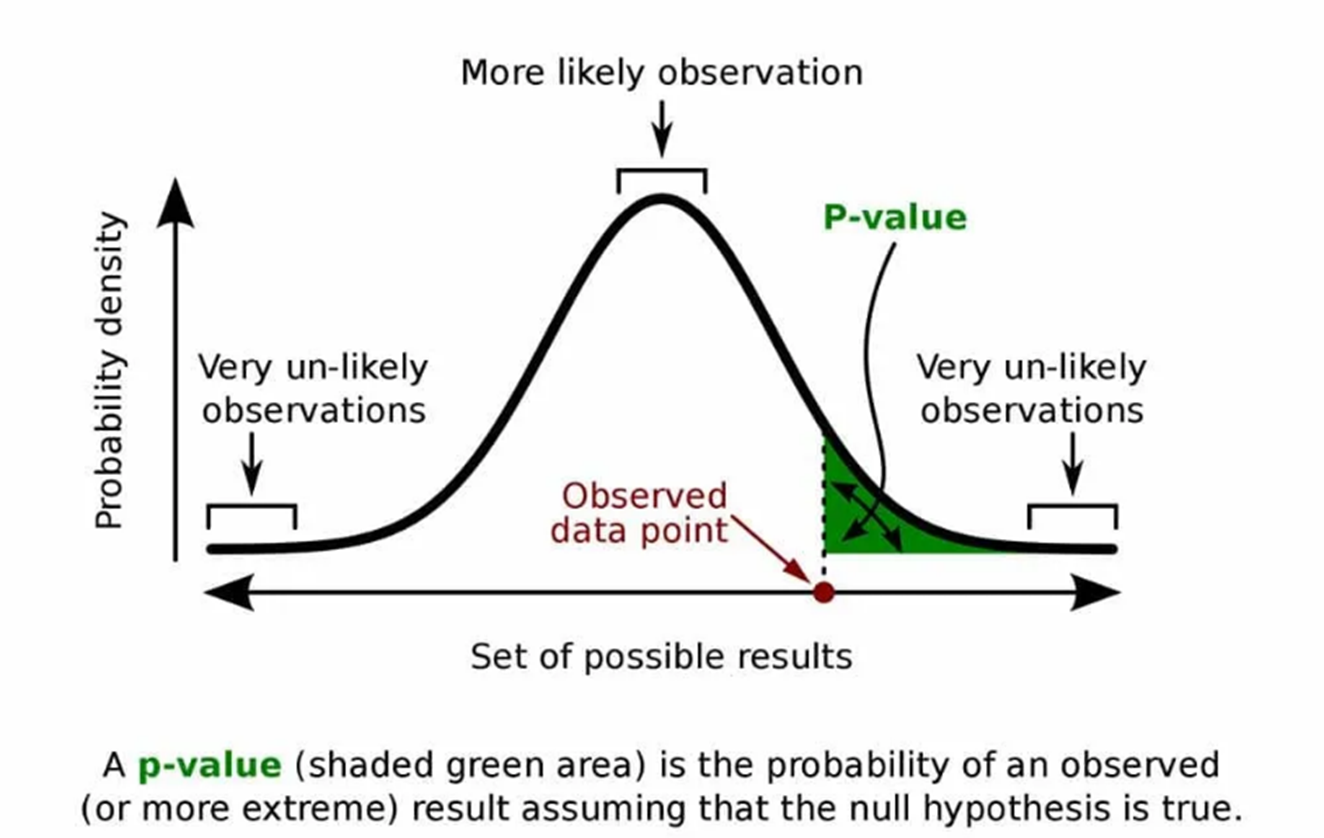
You are planning a clinical trial for your drug. If your results show that the average length of time patients are pain-free is longer for the new drug than that for the standard medicine, how will you know that this is not just a random outcome? If this result falls within the green shaded area of the graph, you may have evidence that your drug has a longer effect. But how can we determine this scientifically? We do this through hypothesis testing.
What is a null hypothesis
Stating your null and alternative hypotheses is the first step in conducting a hypothesis test. The null hypothesis (H0) is what you’re trying to disprove, usually a statement that there is no relationship between two variables or no difference between two groups. The alternative hypothesis (Ha) states that a relationship exists or that there is a difference between two groups. It represents what you’re trying to find evidence to support.
Before we conduct the clinical trial, we create the following hypotheses:
H0: the mean longevity of the new drug is equal to that of the standard drug
Ha: the mean longevity of the new drug is greater than that of the standard drug
Note that the null hypothesis states that there is no difference in the mean values for the two drugs. Because Ha includes “greater than,” this is an upper-tailed test. We are not interested in the area under the lower side of the curve.
Next, we need to determine our criterion for deciding whether or not the null hypothesis can be rejected. This is where the critical p-value comes in. If we assume the null hypothesis is true, how much longer does the new drug have to last?
Let’s say your results show that the new drug lasts twice as long as the standard drug. In theory, this could still be a random outcome, due to chance, even if the null hypothesis were true. However, at some point, you must consider that the new drug may just have a better longevity. The researcher will typically set that point, which is the probability of rejecting the null hypothesis given that it is true, prior to conducting the trial. This is the critical p-value. Typically, this value is set at p = .05, although, depending on the circumstances, it could be set at another value, such as .10 or .01.
Another way to consider the null hypothesis that might make the concept clearer is to compare it to the adage “innocent until proven guilty.” It is assumed that the null hypothesis is true unless enough strong evidence can be found to disprove it. Statistically significant p-value results can provide some of that evidence, which makes it important to know how to calculate p-values.
How to calculate p-values
The p-value that is determined from your results is based on the test statistic, which depends on the type of hypothesis test you are using. That is because the p-value is actually a probability, and its value, and calculation method, depends on the underlying probability distribution. The p-value also depends in part on whether you are conducting a lower-tailed test, upper-tailed test, or two-tailed test.
The actual p-value is calculated by integrating the probability distribution function to find the relevant areas under the curve using integral calculus. This process can be quite complicated. Fortunately, p-values are usually determined by using tables, which use the test statistic and degrees of freedom, or statistical software, such as SPSS, SAS, or R.
For example, with the simplified clinical test we are performing, we assumed the underlying probability distribution is normal; therefore, we decide to conduct a t-test to test the null hypothesis. The resulting t-test statistic will indicate where along the x-axis, under the normal curve, our result is located. The p-value will then be, in our case, the area under the curve to the right of the test statistic.
Many factors affect the hypothesis test you use and therefore the test statistic. Always make sure to use the test that best fits your data and the relationship you’re testing. The sample size and number of independent variables you use will also impact the p-value.
P-Value and statistical significance
You have completed your clinical trial and have determined the p-value. What’s next? How can the result be interpreted? What does a statistically significant result mean?
A statistically significant result means that the p-value you obtained is small enough that the result is not likely to have occurred by chance. P-values are reported in the range of 0–1, and the smaller the p-value, the less likely it is that the null hypothesis is true and the greater the indication that it can be rejected. The critical p-value, or the point at which a result can be considered to be statistically significant, is set prior to the experiment.
In our simplified clinical trial example, we set the critical p-value at 0.05. If the p-value obtained from the trial was found to be p = .0375, we can say that the results were statistically significant, and we have evidence for rejecting the null hypothesis. However, this does not mean that we can be absolutely certain that the null hypothesis is false. The results of the test only indicate that the null hypothesis is likely false.
P-value table
So, how can we interpret the p-value results of an experiment or trial? A p-value table, prepared prior to the experiment, can sometimes be helpful. This table lists possible p-values and their interpretations.
| P-value range | Interpretation |
| p > 0.05 | Results are not statistically significant; do not reject the null hypothesis |
| p < 0.05 | Results are statistically significant; in general, reject the null hypothesis |
| p < 0.01 | Results are highly statistically significant; reject the null hypothesis |
How to report p-values in research
P-values, like all experimental outcomes, are usually reported in the results section, and sometimes in the abstract, of a research paper. Enough information also needs to be provided so that the readers can place the p-values into context. For our example, the test statistic and effect size should also be included in the results.
To enable readers to clearly understand your results, the significance threshold you used, the critical p-value should be reported in the methods section of your paper. For our example, we might state that “In this study, the statistical threshold was set at p = .05.” The sample sizes and assumptions should also be discussed there as they will greatly impact the p-value.
How one can use p-value to compare two different results of a hypothesis test?
What if we conduct two experiments using the same null and alternative hypotheses? Or what if we conduct the same clinical trial twice with different drugs? Can we use the resulting p-values to compare them?
In general, it is not a good idea to compare results using only p-values. A p-value only reflects the probability that those specific results occurred by chance; it is not related at all to any other results and does not indicate degree. So, just because you obtained a p-value of .04 in with one drug and a value of .025 in with a second drug does not necessarily mean that the second drug is better.
Using p-values to compare two different results may be more feasible if the experiments are exactly the same and all other conditions are controlled except for the one being studied. However, so many different factors impact the p-value that it would be difficult to control them all.
Why just using p-values is not enough while interpreting two different variables
P-values can indicate whether or not the null hypothesis should be rejected; however, p-values alone are not enough to show the relative size differences between groups. Therefore, both the statistical significance and the effect size should be reported when discussing the results of a study.
For example, suppose the sample size in our clinical trials was very large, maybe 1,000, and we found the p-value to be .035. The difference between the two drugs is statistically significant because the p-value was less than .05. However, if we looked at the difference in the actual times the drugs were effective, we might find that the new drug lasted only 2 minutes longer than the standard drug. Large sample sizes generally show even very small differences to be significant. We would need this information to make any recommendations based on the results of the trial.
Statistical significance, or p-values, are dependent on both sample size and effect size. Therefore, they all need to be reported for readers to clearly understand the results.
Things to consider while using p-values
P-values are very useful tools for researchers. However, much care must be taken to avoid treating them as black and white indicators of a study’s results or misusing them. Here are a few other things to consider when using p-values:
- When using p-values in your research report, it’s a good idea to pay attention to your target journal’s guidelines on formatting. Typically, p-values are written without a leading zero. For example, write p = .01 instead of p = 0.01. Also, p-values, like all other variables, are usually italicized, and spaces are included on both sides of the equal sign.
- The significance threshold needs to be set prior to the experiment being conducted. Setting the significance level after looking at the data to ensure a positive result is considered unethical.
- P-values have nothing to say about the alternative hypothesis. If your results indicate that the null hypothesis should be rejected, it does not mean that you accept the alternative hypothesis.
- P-values never prove anything. All they can do is provide evidence to support rejecting or not rejecting the null hypothesis. Statistics are extremely non-committal.
- “Nonsignificant” is the opposite of significant. Never report that the results were “insignificant.”
Frequently Asked Questions (FAQs) on p-value
Q: What influences p-value?
The primary factors that affect p-value in statistics include the size of the observed effect, sample size, variability within the data, and the chosen significance level (alpha). A larger effect size, a larger sample size, lower variability, and a lower significance level can all contribute to a lower p-value, indicating stronger evidence against the null hypothesis.
Q: What does p-value of 0.05 mean?
A p-value of 0.05 is a commonly used threshold in statistical hypothesis testing. It represents the level of significance, typically denoted as alpha, which is the probability of rejecting the null hypothesis when it is true. If the p-value is less than or equal to 0.05, it suggests that the observed results are statistically significant at the 5% level, meaning they are unlikely to occur by chance alone.
Q: What is the p-value significance of 0.15?
The significance of a p-value depends on the chosen threshold, typically called the significance level or alpha. If the significance level is set at 0.05, a p-value of 0.15 would not be considered statistically significant. In this case, there is insufficient evidence to reject the null hypothesis. However, it is important to note that significance levels can vary depending on the specific field or study design.
Q: Which p-value to use in T-Test?
When performing a T-Test, the p-value obtained indicates the probability of observing the data if the null hypothesis is true. The appropriate p-value to use in a T-Test is based on the chosen significance level (alpha). Generally, a p-value less than or equal to the alpha indicates statistical significance, supporting the rejection of the null hypothesis in favour of the alternative hypothesis.
Q: Are p-values affected by sample size?
Yes, sample size can influence p-values. Larger sample sizes tend to yield more precise estimates and narrower confidence intervals. This increased precision can affect the p-value calculations, making it easier to detect smaller effects or subtle differences between groups or variables. This can potentially lead to smaller p-values, indicating statistical significance. However, it’s important to note that sample size alone is not the sole determinant of statistical significance. Consider it along with other factors, such as effect size, variability, and chosen significance level (alpha), when determining the p-value.
Researcher.Life is a subscription-based platform that unifies the best AI tools and services designed to speed up, simplify, and streamline every step of a researcher’s journey. The Researcher.Life All Access Pack is a one-of-a-kind subscription that unlocks full access to an AI writing assistant, literature recommender, journal finder, scientific illustration tool, and exclusive discounts on professional publication services from Editage.
Based on 21+ years of experience in academia, Researcher.Life All Access empowers researchers to put their best research forward and move closer to success. Explore our top AI Tools pack, AI Tools + Publication Services pack, or Build Your Own Plan. Find everything a researcher needs to succeed, all in one place – Get All Access now starting at just $17 a month!




